is a Computational Fluid Dynamics (CFD) Engineer who joined ENA2 in July 2020. He received his Ph.D. from the University of Calgary and was a postdoctoral research fellow at the University of Alberta before joining the team.
Lattice Boltzmann Method in a nutshell
Due to the rapid advancement in computational power of modern computers, the desire for computational analysis of fluid flow, heat transfer and other related phenomena is growing in different industries. According to the IMARC market research group [1], the global CFD market reached a value of US$1.9 Billion in 2020 and is expected to grow moderately during the next five years. This growing interest for CFD analysis has led to a rapid development in the number of open source and commercial CFD solvers. Dassault Systemes’ SIMULIA brand started to develop its own mainstream CFD solver based on the finite volume method in 2014. This was followed by two acquisitions which brought in high fidelity Lattice-Boltzmann based flow solvers: Next Limit Dynamics with XFlow in 2016 and Exa corporation with PowerFlow in 2017. To survive in current competitive market, CFD solvers should demonstrate specific features to be distinguished from others. XFlow and PowerFlow are discerned by their Lattice Boltzmann technology. This article will briefly cover how a solver uses this technology to perform CFD simulations.
The Lattice Boltzmann Method (LBM) is a relatively new flow simulation technique that solves the Lattice Boltzmann (LB) equation in the domain of interest instead of direct solution of the Navier-Stokes (NS) equations. Fig. 1 shows different approaches at different scales to perform flow simulations. In the macroscopic scale, where the continuum mechanics and NS equations are valid, conservative equations of fluid properties are directly solved in polyhedral mesh. In the microscopic scale, the motion of individual fluid molecules and their interactions with each other are solved, governed by Newton’s dynamics. LBM however, is developed in an intermediate mesoscopic scale and does not track individual molecules nor directly solves for the macroscopic variables. Rather, it tracks a representative collection of fluid molecules in the domain in terms of their population. Clearly, a population of fluid particles represents fluid density. Therefore, by tracking the fluid particles population, the LB equation actually solves for the fluid density in the domain.
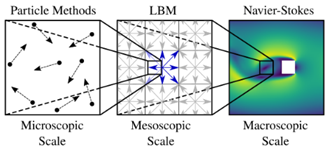
Fig. 1 Lattice Boltzmann within scale frame [2]
In LBM, the domain is discretized in small voxels rather than arbitrary polyhedral mesh. Those voxels or lattices are representative of the collection of fluid particles that occupy small portion of the domain. As mentioned, LB equation solves for the fluid density in each voxel. But since fluid particles have random motions, the density of the fluid in the voxel is variable in infinite directions. So, to discretize this continuous property for numerical simulations, it is assumed that density has a number of components equal to the number of vectors in each voxel. Those vectors represent discrete velocity directions of the collection of particles in the voxel. The number of discrete velocity vectors and discrete density components in the voxel are equal.
To minimize memory, as few velocities as possible is desirable. However, there is a tradeoff between smaller velocity sets and higher accuracy [3]. Note that those velocity sets are called lattice velocities and are different than the macroscopic velocity of the fluid in the lattice. The length and direction of the lattice velocities for different velocity sets are reported in references [3]. All components of the lattice velocity vectors are integer multiples of 
, where 
and 
are space and time resolutions in any set of units.
How are the fluid particles distributed in the voxel and in the domain? According to the Lattice Boltzmann equation, it consists of two parts: collision of fluid particles in the voxel and their streaming to the neighboring voxels. With this explanation, the interpretation of the LB equation is straightforward:
(1)
represents the density of the fluid particles moving with lattice velocity 
and 
is the collision operator. Subscript 
represents the number of density or lattice velocity components in the voxel. According to the LB equation, the density of fluid particles with velocity at neighboring voxel x +
and at time 
is equal to their density at previous time step at location x, plus any effect resulting from particle collision. Different collision operators are reported in the literatures [3] and it is still the subject of research in academia.
After finding all components of the fluid density in the voxel by solving the LB equation, the total density is simply calculated by adding all density components in the voxel: 
(2)
and lattice velocity sets 
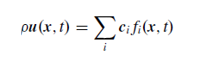
(3)
Implementing LBM is quite simple as the solver bypasses complicated iterations to deal with non-linear terms. It is easy to run on parallel architectures as the heaviest computations in LBM is local. LBM is well suited to simulate flows in complex geometries, very effective in multiphase and multicomponent flows, extremely efficient in computational aeroacoustics, very promising to deal with moving boundaries, and is generally appropriate to simulate mesoscopic physics that are hard to describe macroscopically. These advantages, among others, make LBM very attractive for XFlow and PowerFlow developers.
References
[1] IMARC Group. Computational fluid dynamics market: Global industry trends, share, size, growth, opportunity, and forecast 2021–2026. https://www.imarcgroup.com/computational-fluid-dynamics-market
[2] Bravo, A.A.C.P., 2000. Wind Flow Simulation around Buildings using the Lattice Boltzmann Method. Int. J. Heat and Fluid Flow, 21, pp.186-196.
[3] Krüger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G. and Viggen, E.M., 2017. The lattice Boltzmann method. Springer International Publishing, 10 (978-3), pp.4-15.
